Nuclear Power

Thermodynamic processes are governed by the laws of conservation of mass and conservation of energy except for the special case NUCLEAR REACTION.



Since the early 1950s, nuclear fission technology has been explored on a large scale for electrical power generation and has evolved into the modern power plant. Many advantage of nuclear energy are not well understood by the general public, but this safe, environmentally benign source of electricity is still likely to play a major role in the world. Nuclear electric power generation is ideally suited to provided large amounts of power whole minimizing the overall environmental impact.


The initial peaceful application poctulated a controlled nuclear fission chain reaction, generating heat in the fuel and transferring the heat through a fluid medium to a heat exchanger to a produce steam.

Nuclear energy is derived from the conversion of very small amount of mass into large amounts of energy, following Albert Einstein's famous relationship E = m.c^2.

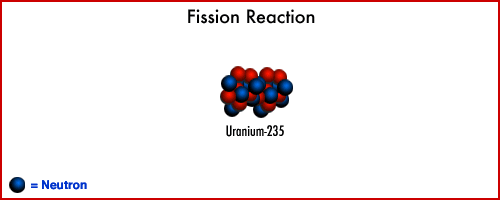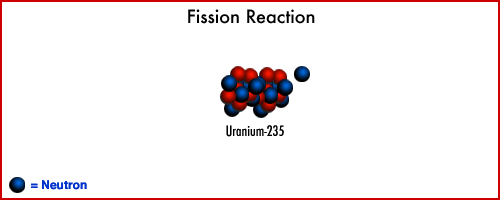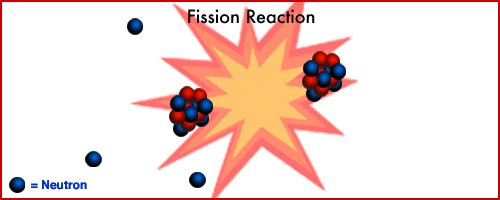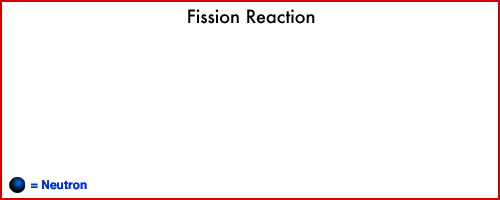
The nuclear reaction in today's commercial reactors are based upon a multi-step fission or atom splitting process. Neutrons are absorbed by the fissionable atom which usually U-235. The atom becomes unstable and break apart or fission to typically produce two large pieces (new atom), two or more neutrons and some radiation. The mass of the resulting products is less than that of initial material by a small amount.

This change in the mass produces energy which predominantly takes the form of kinetic energy of the product particle plus some radiation. The kinetic energy eventually appears as internal heating of the fuel which serve as the heat source for the ultimate steam power generation cycle. The neutrons produced serve as the input to the next fission reaction resulting in a chain reaction. A critical mass is achieved when enough nuclear material or brought together so that the fission reaction continue without an external supply of neutrons.

Fission compare to Fusion
The fission of U235 produces about 200 MeV of energy.
Since the reactantants have a mass of 236 amu [ 235 from the uranium and 1 from the neutron ] the energy produced per unit mass is

E/M = 200 MeV / 236 amu = 0.85 MeV/amu

Now let's look at D-T fusion as illustration animation below this. D-T fusion releases 17.6 MeV of energy while the mass of the reactants is 5 amu [ 2 from D, 3 from T] Hence,

E/M = 17.6 MeV/ 5 amu = 3.52 MeV/amu

which is about 4.1X the analogous E/M ratio for fission above. [ So it looks like fusion is more powerful]



So fission gives you more energy per reaction - but fusion gives you more energy per unit mass for these reactions.

Why the energies [ 200 MeV for fission and 17.6 MeV for fusion ] are what they are is that they are the difference in the masses between the reactants and products.

If you take the mass of D, add the mass of T, subtract the mass of He4 and subtract the mass of a neutron, then multiply by the square of the speed of light [ E=mc^2] you will get 17.6 MeV.

For detail info, please click here.